The Sargent 2-stage function

This function calculates sample sizes of the Sargent 2-stage design.

The goal of a phase II trial is to make a preliminary determination regarding the activity and tolerability of a new treatment and thus to determine whether the treatment warrants further study in the phase III setting.
This function calculates the sample size needed in a Sargent 2-stage design which is a three-outcome design that allows for three outcomes: reject \(H(0)\), reject \(H(a)\), or reject neither.

sargent2stage(
  p0,
  pa,
  alpha,
  beta,
  eta,
  pi,
  eps = 0,
  N_min,
  N_max,
  int = 0,
  int_window = 0.025,
  CI_type = "Koyama"
)

Arguments

p0

probability of the uninteresting response (null hypothesis \(H0\))
pa

probability of the interesting response (alternative hypothesis Ha)
alpha

Type I error rate \(P(reject H0|H0)\)
beta

Type II error rate \(P(reject Ha|Ha)\)
eta

\(P(reject Ha|H0)\)
pi

\(P(reject H0|Ha)\)
eps

tolerance default value = 0.005
N_min

minimum sample size value for grid search
N_max

maximum sample size value for grid search
int

pre-specified interim analysis percentage information
int_window

window around interim analysis percentage (e.g. 0.5 +- 0.025). 0.025 is default value
CI_type

"Koyama", see getCI_Koyama, or any type for binom.confint

Value

a data.frame with elements

  • n1: total number of patients in stage1

  • n2: total number of patients in stage2

  • N: total number of patients=n1+n2

  • r1: critical value for the first stage

  • r2: critical value for the second stage

  • eff: s/N

  • CI_LL: (1-2*alpha) CI lower limit

  • CI_UL: (1-2*alpha) CI upper limit

  • EN.p0: expected sample size under H0

  • PET.p0: probability of terminating the trial at the end of the first stage under H0

  • MIN: column indicating if the design is the minimal design

  • OPT: column indicating if the setting is the optimal design

  • ADMISS: column indicating if the setting is the admissible design

  • alpha: the actual alpha value which is smaller than alpha_param + eps

  • beta: the actual beta value where which is smaller than beta_param + eps

  • eta: the actual eta value which is smaller than eta_param - eps

  • pi: the actual pi value which is smaller than pi_param - eps

  • lambda: 1-(eta+alpha)

  • delta: 1-(beta+pi)

  • p0: your provided p0 value

  • pa: your provided pa value

  • alpha_param: your provided alpha value

  • beta_param: your provided beta value

  • eta_param: your provided eta value

  • pi_param: your provided pi value

Details

if x1<=r1 --> stop futility
if (x1+x2)<=r --> futility
if (x1+x2)>=s --> efficacy

References

Sargent DJ, Chan V, Goldberg RM. A three-outcome design for phase II clinical trials. Control Clin Trials. 2001;22(2):117-125. doi:10.1016/s0197-2456(00)00115-x

Examples

samplesize <- sargent2stage(p0 = 0.1, pa = 0.3, alpha = 0.05, beta = 0.1, eta = 0.8, pi = 0.8,
                            eps = 0.005, N_min = 15, N_max = 30)
plot(samplesize)


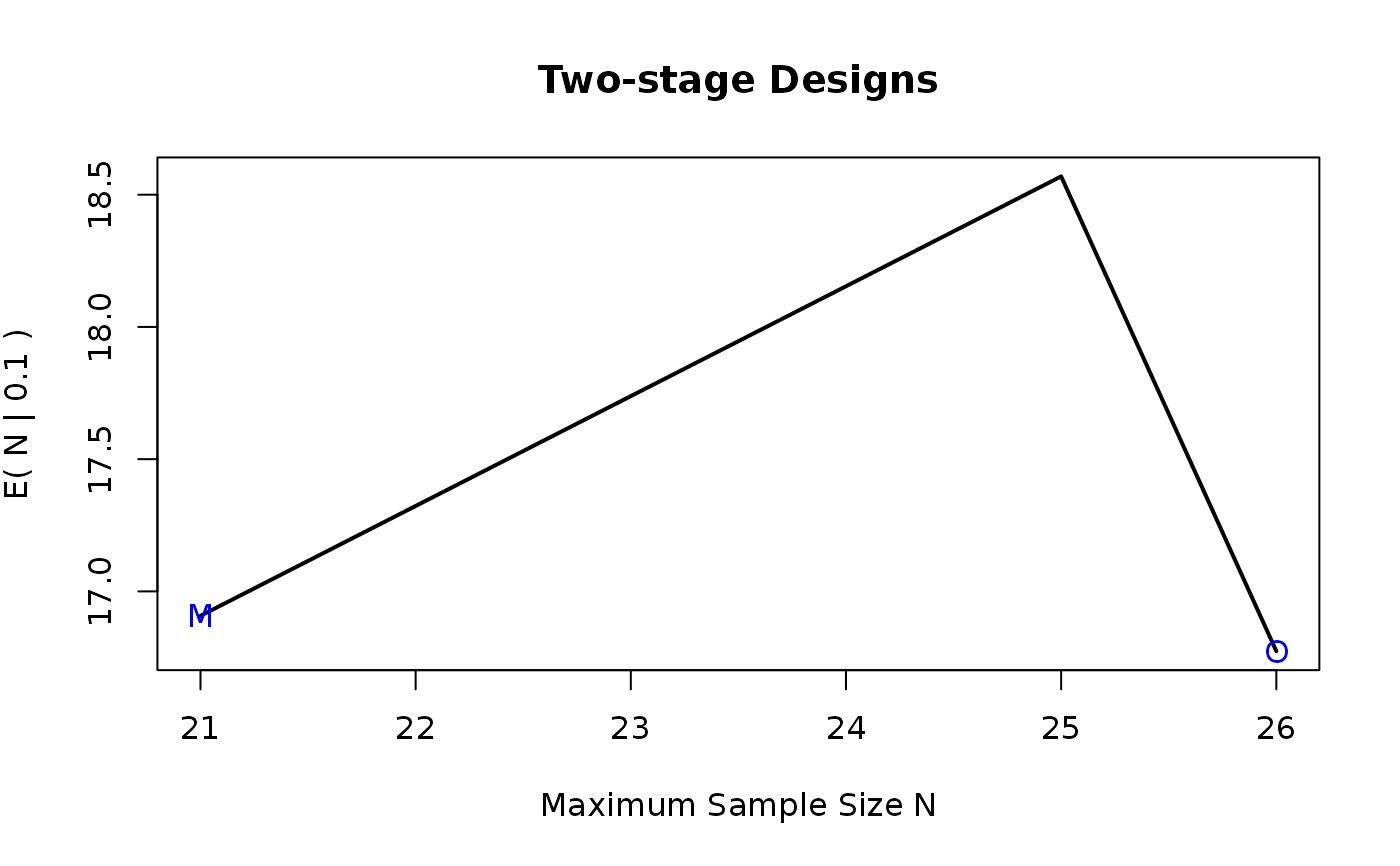# \donttest{
data(data_sargent2)
test <- data_sargent2
samplesize <- sargent2stage(p0 = test$p0, pa = test$pa, alpha = test$alpha, beta = test$beta,
                            eta = test$eta, pi = test$pi,
                            eps = 0.005,
                            N_min = test$N_min, N_max = test$N_max)
optimal <- lapply(samplesize, FUN=function(x) subset(x, OPT == "Optimal"))
optimal <- data.table::rbindlist(optimal)
#> Column 9 ['90%CI_LL'] of item 2 is missing in item 1. Use fill=TRUE to fill with NA (NULL for list columns), or use.names=FALSE to ignore column names. use.names='check' (default from v1.12.2) emits this message and proceeds as if use.names=FALSE for  backwards compatibility. See news item 5 in v1.12.2 for options to control this message.
minimax <- lapply(samplesize, FUN=function(x) subset(x, MIN == "Minimax"))
minimax <- data.table::rbindlist(minimax)
#> Column 9 ['90%CI_LL'] of item 2 is missing in item 1. Use fill=TRUE to fill with NA (NULL for list columns), or use.names=FALSE to ignore column names. use.names='check' (default from v1.12.2) emits this message and proceeds as if use.names=FALSE for  backwards compatibility. See news item 5 in v1.12.2 for options to control this message.
# }